Здравствуйте. Сегодня мы поговорим о самоподобии и закономерностях, которые нас окружают. Как можно вообразить бесконечность вселенной? Присаживайтесь поудобнее.
МАТЕМАТИКА – ЭТО КРАСИВО
Математика. Как вы относитесь к ней? Имеете ли вы глубочайшие знания в этой науке или, быть может, теряетесь от базовых задач? Во втором случае, конечно, вам будет тяжеловато в ХНУРЭ. Интересен другой момент, вы либо находите это красивым, либо же - нет.
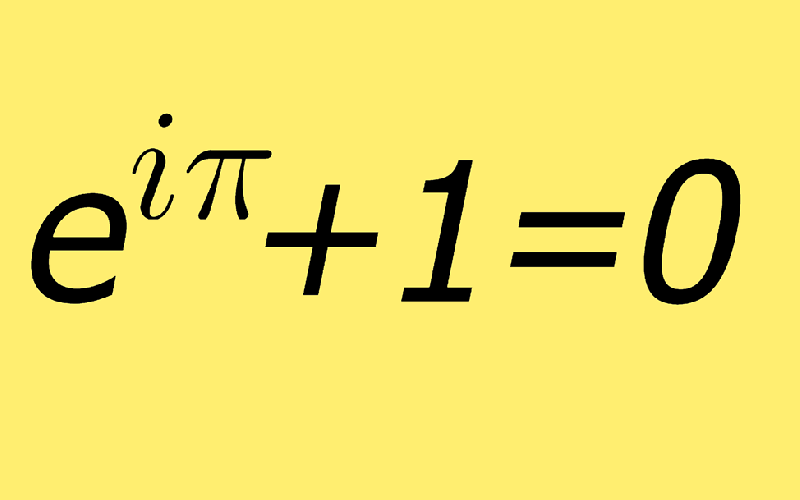
Как вам? Это частный случай тождества Эйлера. Ричард Фейман, великий физик, назвал это «нашим сокровищем». Если эта формула вам не по душе, то математикам всего мира вам больше нечего предложить. Хотя, дайте мне еще один шанс.
САМОПОДОБИЕ В ДЕТАЛЯХ
В 1883 ГОДУ ГЕОРГ КАНТОР описал некий математический объект. Это бесконечное объединение подмножеств единичного отрезка, а вот и он сам.
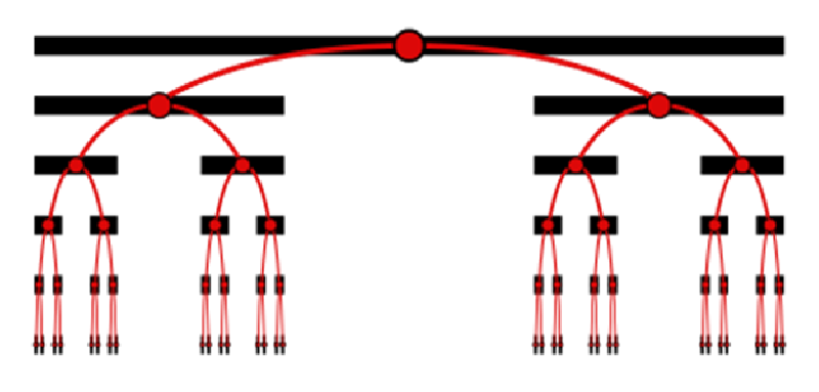
Так, красных линий быть не должно, но вы потом поймете, зачем они. Научить делать эту красоту?
- Нарисуйте отрезок, ага?
- Визуально разделите его на три равных отрезка и два крайних нарисуйте чуть ниже.
- И это, повторите для каждого отрезка, пока результат вас не устроит.
При масштабировании этого объекта, его структура не будет упрощаться – напротив он будет похож сам на себя.
Ладно, это не самое красивое и для меня, признаюсь. Но чего вы хотели от девятнадцатого века? Да, и надо было с чего-то начинать.
ВЫ ЭТО МОЖЕТЕ ПОВТОРИТЬ ИЛИ СДЕЛАТЬ ЛУЧШЕ
Сейчас я покажу уже нечто интересное. Вот такой вывод сделала моя программа. В ней я создал наложение неких фигур и инвертировал цвета. Вот, что у меня вышло в итоге:

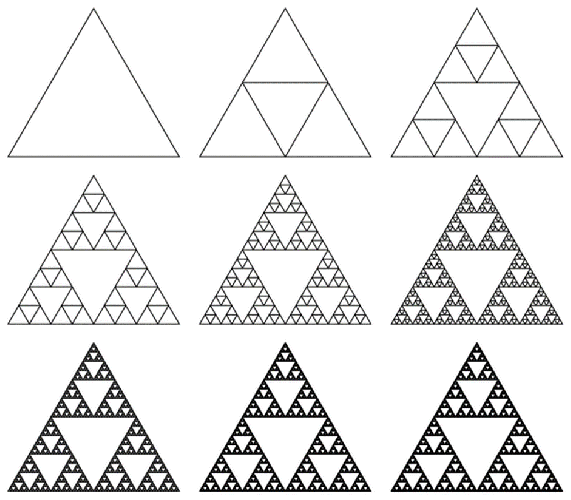
ТРЕУГОЛЬНИК СЕРПИНСКОГО
Знакомьтесь, треугольник Серпинского – еще одно самоподобное множество. В моем случая, он построен способом Хаоса, ниже – итераций. Подробнее об этом вы можете узнать в Википедии.
МНОЖЕСТВО БЕНУА МАНДЕЛЬБРОТА
Ну, а теперь давайте же назовем все фигуры, которые обладают этим самым самоподобием и нетривиальной формой. К счастью, за нас это сделал Бенуа Мандельброт в 1975 году. И имя таким объектам – фракталы.

Это множество Мандельброта, хотя сам Бенуа впервые увидел свой фрактал в таком виде:

Не будем вдаваться в подробности, как это выходит. Детали вы можете увлекательно изучить на сайте: sunandstuff.com/mandelbrot/about/
ПРЕДВИДЯ СКЕПСИС. КАСКАД БИФУРКАЦИЙ
Если вас смущают комплексные числа и кажется, что все это ерунда, которая на практике не имеет вообще никакой связи с реальным миром, то смею вас огорчить. Вспомните те ненужные красные линии в множестве Кантора. И посмотрите сюда — это каскад бифуркаций.
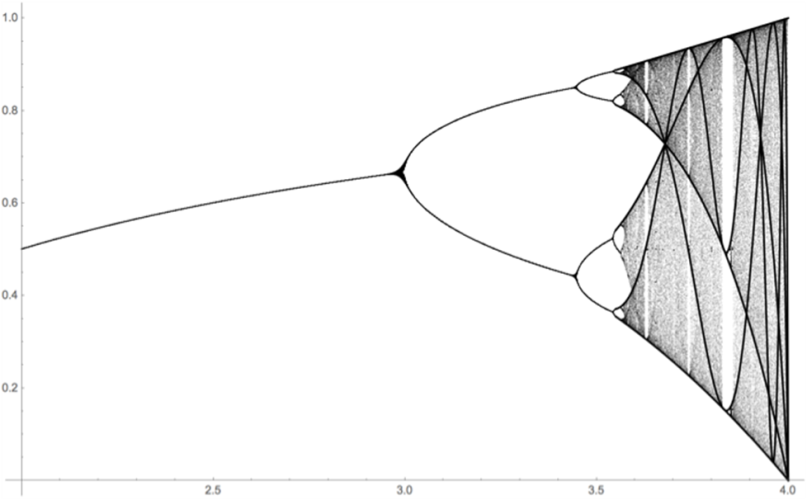
Такое множество точек можно получить из любой функции с одним максимумом. Каскад бифуркаций может изображать изменения в популяции кроликов, тепловую конвекцию в жидкости и даже… ритм протекающего крана, но самое интересно – это связь с множеством Мандельброта.


Еще не видите это? А так?

Теперь, если вас не впечатлила та формула из начала статьи, то фракталы точно должны сделать свое дело.
Подробнее про формулу каскадов бифуркации и постоянную Фейгенбауматут:youtube.com/watch?v=DH1cv0Rdf2w&t=760s
ЗАКЛЮЧЕНИЕ
И вот, когда я уже готов было начать писать эту статью, мне в голову пришла забавная аналогия. Я думаю, вы видели, как на разных моделях наше пространство масштабируется, начиная с нашей планеты и заканчивая некими волокнами материи, где все галактики смешиваются в кашу. Это, в целом, псевдонаучно, но… Мне лестно верить, что мы с нашим миром всего лишь одно целое, одна самоподобная вселенная.
DarkMinimum